创新物理习题教学
长汀一中 罗春春
我们知道习题教学对帮助学生掌握和巩固物理概念和规律，培养能力都有莫大的作用，它也是新课程中实现“三维目标”的必要手段和途径。笔者在平时物理习题教学尤其是多年高考物理复习中的习题讲评中积累了一些体会。
一、习题教学前应先选好题、做好题
目前教学中的习题多如牛毛，良莠不分。这样用的现成资料容易造成习题机械重复，加重学生的练习负担，同时题目本身及其答案的错误和疏漏也时有发生，如果随便发一张试卷，布置一点练习，结果发现有错题，那不仅浪费了宝贵的学习时间，而且也会对老师产生负面影响。关于这一点我们是这样做的：尽量少用现成资料，用剪贴练习，剪贴之前老师先自己做过，这样做有很多好处。
“学生独立做，老师看着答案做。” ——这是司空见惯的现象，很少有老师是独立做的，美其名曰为节省时间而抵御不了答案诱惑一睹为快，这样，久而久之解题就会找不到感觉，对答案更具依赖性。“不要看人家的答案包括教学参考书。要答案，自己做！！！”
老师多做题，是为了学生少做题。老师多做题，是为了给学生讲好题。老师多做题，是为了让学生会做题。总之，做了再说。
二、习题教学中模型化思想的运用
一般的物理习题都是拟题者根据自己头脑中的一个理想化物理模型，结合某些问题情境和物理条件而拟定出来的。解题过程就是还原拟题者物理模型的过程，也就是把实际问题模型化，把具体问题抽象成熟悉的典型物理问题的过程。这种模型化的方法是物理解题中的一种普遍方法。
例1 如图1所示，劲度系数为k的弹簧一端固定于墙壁，另一端系着质量为M的物体，物体静止于光滑水平面O点处，现在一质量为m的子弹以水平速度v0射进且留在物体中，试问碰撞后物体的速度？物体的最大位移是多少？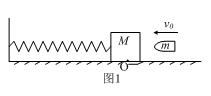
析与解 开始时取子弹和物体组成的系统为研究对象，忽略子弹的转动，认为子弹射进物体的过程为平动，从而建立质点系统模型。因为从子弹开始射进物体到停留在物体中这一过程时间极短，弹簧的形变微小到可以忽略，所以可认为在此过程中，沿水平方向系统所受合外力为零，系统的变化为完全非弹性碰撞过程，从而可建立完全非弹性碰撞过程模型且系统动量守恒，故有
又系统获得速度v的过程短暂，它们的位移微小到可以忽略，故可认为系统虽已具有速度v，但还处在平衡位置Ｏ点处。此后，选子弹、物体和弹簧组成的系统为研究对象，忽略弹簧质量、空气阻力与摩擦力，建立弹簧振子模型；振子从平衡位置Ｏ处以速度v向左运动过程满足简谐运动规律，故可得方程
即可求得物体的最大位移s为
在求解这个题目中，先后建立了两个研究对象的理想化模型（相互作用的质点系及弹簧振子）和两个运动变化过程理想化模型（完全非弹性碰撞及简谐运动），这些模型一旦建立，学生就知道用动量守恒和简谐运动的公式求解并得出相应的结果。
三、习题教学与探究实验的结合
如静摩擦力方向的判别是学生学习中的难点，其主要原因是学生缺乏对日常生活的感性认识，很难想像两个相对静止而又有相对运动趋势的物体接触面间静摩擦力的方向。在教学中可取两只鞋刷，将其中一只固定在台面上，另一只叠放在它的上面，并水平推动该鞋刷，可看到上、下物体间刷毛形变的方向相反，由此可推想出上、下鞋刷所受静摩擦力的方向。这既给学生提供了一个表象思维的模型，化抽象为形象，又能培养学生的创新能力。
例2 如图2所示为一个边长为a的大正方体木箱，有一只老鼠从顶角Ａ处出现后发现了一只猫。老鼠要从Ａ处沿木箱表面逃到位于顶角Ｇ处的鼠洞。设老鼠爬行的速度为v，则老鼠从Ａ到Ｇ至少需要多少时间？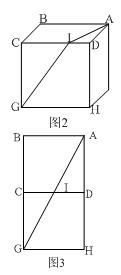
老鼠从Ａ处可以选择正方体不同的面到达Ｇ处，即使选择了某两个面，如ＡＢＣＤ面和ＣＤＨＧ
面，也需要考虑当Ｉ点应当选择不同的位置时，行进的路线就不同。那么Ｉ点应当选择在哪一个位置，才能使行进的路线ＡＩＧ耗时最少呢？
由于老鼠的运动速度保持不变，所以，要使耗时最少，应使老鼠行走的路线最短。于是问题就归结为寻找一条能够连接Ａ、Ｇ两点最短的路线。为此，可以取一个正方体纸盒，将其中两个侧面剪出来并压平，如图3。显然，图上直线段ＡＧ就是Ａ、Ｇ两点最短的路线。于是就有
进而知老鼠从Ａ到Ｇ至少需要的时间为
四、习题教学与多媒体的结合
多媒体作为现代教育的辅助工具，它可显示传统演示教具中无法涉及的地方。如：对于某些物理现象，条件不易控制或存在某些干扰而无法演示；实验时动态太快无法看清过程，用传统的教学手段也很难表现“动”和“变”的结果。此时若用计算机来模拟物理过程和物理情景，并将过程进行重放、定格、缩放、慢镜头，让学生观察物理全过程。用多媒体作为辅助习题教学的工具和手段，可以充分发挥它的优势，弥补学生直观感觉的不足，减低抽象思维的难度，展示物理情景，帮助学生建立物理模型，以便于顺利解题。
例3 在原子核物理中，研究核子与核关联的最有效途径是“双电荷交换反应”。这类反应的前半部分过程和下述力学模型类似。两个小球A和B用轻质弹簧相连，在光滑的水平直轨道上处于静止状态。在它们左边有一垂直于轨道的固定挡板P，右边有一小球C沿轨道以速度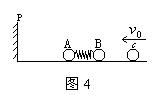
C与B发生碰撞并立即结成一个整体D。在它们继续向左运动的过程中，当弹簧长度变到最短时，长度突然被锁定，不再改变。然后，A球与挡板P发生碰撞，碰后A、D都静止不动，A与P接触而不粘连。过一段时间，突然解除锁定（锁定及解除定均无机械能损失）。已知A、B、C三球的质量均为m。
（1）求弹簧长度刚被锁定后A球的速度。
（2）求在A球离开挡板P之后的运动过程中，弹簧的最大弹性势能。
此题首先应审清题意，明确物理过程，建立物体运动情景，而要建立清晰的运动则必须搞清C与B发生碰撞前后的运动情况以及解除锁定之后它们怎样运动？笔者在讲评该题时，借助Ｆlash动画模拟整个运动过程，收到良好效果。学生自己分析出解题思路：
考察Ａ、Ｂ、Ｃ及弹簧组成的系统。
全过程中，有两个分过程机械能（动能与弹性势能之和）不守恒：Ｃ与Ｂ结合过程、Ａ与Ｐ碰撞过程。全过程中，有两个分过程动量不守恒：Ａ与Ｐ碰撞的过程、解除锁定后弹簧恢复自然长度的过程。
C与Ｂ结成整体Ｄ的过程，动量守恒，可求出结合后瞬时整体Ｄ的速度；从弹簧开始缩短，到长度被锁定（Ａ、Ｄ具有相等速度），动量守恒，机械能也守恒，可求出共同速度，可求出弹簧在锁定状态下的弹性势能；从解除锁定到弹簧恢复到自然长度，机械能守恒，可求出弹簧恢复自然长度时Ｄ的速度；从弹簧恢复到自然长度，到Ａ、Ｄ达到相等速度，动量守恒，机械能也守恒，可求出共同速度，并求出此时弹簧的弹性势能——离开档板后弹簧的最大弹性势能。最后答案为：
五、错解资源的利用
建构主义学习观认为，学生的错误不可能单靠正面示范和反复练习去纠正，必须通过主体对于自身认知活动的自我意识、自我评价、自我调整去加以纠正。作为教师，应机智、灵活地引导学生去修正错误，引领学生从错中求知，从错中探究。
例4 如图5，
质量为
本题是2005年全国高考理综第I卷第24题，我省改卷反馈的情况：本题难度为0.2216，平均得分为4.21分（满分为19分）是试卷中难度最大的试题，同时所反映的错误问题也最多。最典型的思维障碍是：挂上
［情景1］ 竖直上抛的物体到达最高点时是否处于平衡状态。
［情景2］ 做简谐运动的单摆在振幅位置时（最大摆角为θ）是否处于平衡。
［情景3］ 如图6所示，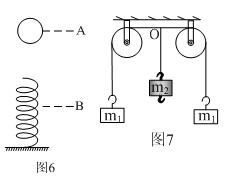
轻弹簧一端固定于地面，小球从一定高度静止释放，小球接触弹簧并压至最低点Ｂ，在Ｂ位置时是否处于平衡。
［情景4］ 如图7所示，两个质量为m1的物体通过轻绳挂于光滑滑轮上，质量为m2的物体挂于轻绳的中间，不计所有的阻力且有m2> m1，当m2落至最低点时是否处于平衡状态。
［情景5］ 如图8所示，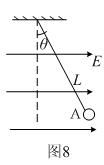
在匀强电场Ｅ中用丝线悬挂的带电小球Ａ，质量为m、带电量为＋q，丝线长为Ｌ，从竖直位置静止释放后，达到最大偏角为θ时是否处于平衡状态。
通过对述情景的状态特征分析，引发学生的“观念冲突”——原题中Ｃ到达最低点时是否处于平衡状态？速度为零一定是平衡状态吗？对已形成的知识从另一个角度以另一种方式进行全新的再思考，既有利于问题的解决，又培养了学生的反思能力，促进了学生元认知的发展。
再引导学生用能量规律（系统机械能守恒）解决该题，那就水到渠成了。
限于篇幅，笔者在这里就不讨论我们在习题教学中常见的方法如一题多变、一题多用、一题多解等问题。
上述对物理习题教学的“创新经营”，无论从知识点的掌握上，还是从解题思维的深入上看，都能收到固本拓新之效，最终达到提高分析和解决问题的能力以及发展学生思维的目的。
